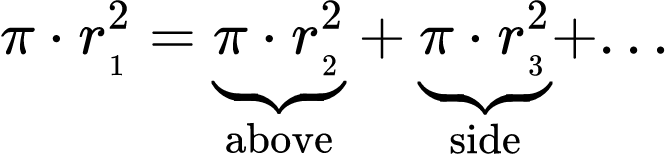Da Vinci’s rule of trees
“All the branches of a tree at every stage of its height when put together are equal in thickness to the trunk. All the branches of a water at every stage of its course, if they are of equal rapidity, are equal to the body of the main stream.”
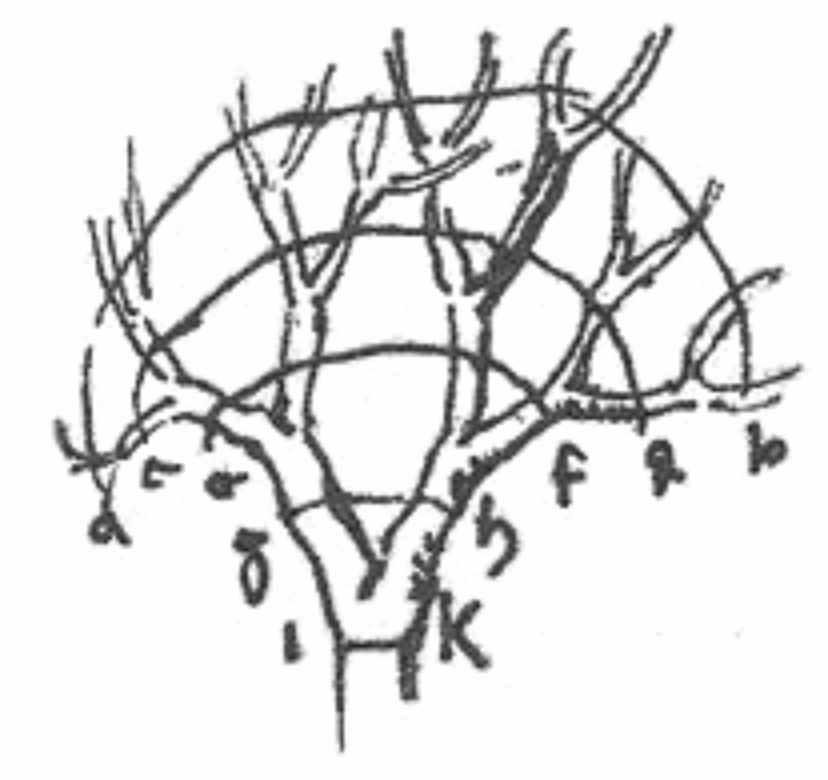
A good 500 years ago, Leonardo da Vinci turned his eyes to trees and made these intriguing observations. This comes from a collection of notes that was intended as a guide for artists on how to draw and paint natural looking trees, but they have since inspired many people who want to understand trees, including yours truly. Leonardo accompanied what is now known as his “rule of trees” with the drawing to the right.
Da Vinci threw together all branches at once, but the same rule also applies to each single branching point: the cross sections of the two branches above a branching point add up to the single cross section below that point. Starting from the tip of each branch, every side branch adds thickness and builds up to the trunk.
We can simplify this equation by removing all occurrences of π. You see that I replaced the exponent of 2 with the variable α. Da Vinci sticked to the square exponent of 2, resulting in the area of the cross section. But following scientists found out that in real trees, this exponent varies between 1.8 and 3.0, which results in different tree shapes. That makes the concept a bit weird. When using an exponent of 1, the formula simply adds up the radius of the above branches. Moving to an exponent of 2, it adds the areas like da Vinci observed. And all the way up to 3, it kind of adds up some strange version of local volume I guess… It gets hard to conceptualize. But it works, well kind of…
500 Years later…
Above all, using da Vinci’s rule, the trees look very naturalistic. That was da Vinci’s whole point; teaching fellow artists how to paint convincing trees. But does the rule hold up in a physical simulation like The Grove?
For the past 9 years, The Grove has been using da Vinci’s rule to thicken the branches on your trees. Using the
Join slider, you can tweak the exponent to increase the buildup of thickness, and it looks really convincing. But when you add physics, any change in thickness also strongly influences the character of the tree. This is what creates weeping willows at one end and strong oaks on the other.
Where the rule works really well for some trees, it works quite badly for others. So through the years I have complicated the thickening code with things like Reduce and Deadwood. Reduce means that new side branches grow thinner with a decrease in growth power. And deadwood will add thickness with each dropped branch. Each of these are real things, but they didn’t help the simulation to grow the tree characters I was after.
After growing thousands upon thousands of trees, I have come to the conclusion that
the rule works well for older, thicker branches and the trunk, but not so well for thin, new growth. The correct thickening of older branches is what makes it look so very natural, but it’s the thinner branches that build the character of the tree. Early on in development, branches are relatively thin and bend much more and even tiny differences in the buildup of thickness will cause a different shape of tree.
Reaction wood, too, is strongly dependent on how fast a branch grows thicker. Like with bending, even the slightest shift in when thickness starts to increase will alter the tree shape considerably.
Da Vinci made an awesome start with his observation, but instead looking at the eventual effect, we need to turn our eyes to the actual cause, the reason why branches grow in thickness. To be continued…